Answer:
The 8th term of the sequence is 896/2187.
Explanation:
We want to find the 8th term of a geometric sequence whose common ratio is 2/3 and whose first term is 7.
We can write a direct formula. Recall that the direct formula of a geometric sequence is given by:
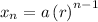
Where a is the initial term and r is the common ratio.
Substitute:
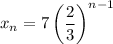
To find the 8th term, let n = 8. Substitute and evaluate:

In conclusion, the 8th term of the sequence is 896/2187.