Answer:
Relation is a function.
Since x is in between -2 and -1 but can also equal them :
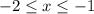
Since y is in between -2 and 2 but can also equal them :
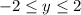
Explanation:
Hey there! To solve this question we first need to figure out the two points marked on the graph.
Point 1 (Bottom point): (-2,-2)
Point 2 (Top point): (-1,2)
Since x is the domain and y is the range...
Graph shows that the 2 domains are -2 & -1
Graph shows that the 2 ranges are -2 and 2
With this information we can create an inequality for x and y...
Since x is in between -2 and -1 but can also equal them :
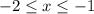
Since y is in between -2 and 2 but can also equal them :
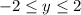
Since the 2 domains don't match, this relation is a function
Hope I helped! :)