Question

each graph shows a relation. The first and second numbers of each ordered pair in the relation are members of the set of real numbers. find the range and domain of the relation. Please explain how you did it instead of just giving an answer

Answer 1

Relation is a function.

Since x is in between -2 and -1 but can also equal them :
`-2\leq x\leq -1\\`

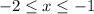
Since y is in between -2 and 2 but can also equal them :
`-2\leq y\leq 2`

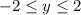
Explanation:

Hey there! To solve this question we first need to figure out the two points marked on the graph.

Point 1 (Bottom point): (-2,-2)

Point 2 (Top point): (-1,2)

Since x is the domain and y is the range...

Graph shows that the 2 domains are -2 & -1

Graph shows that the 2 ranges are -2 and 2

With this information we can create an inequality for x and y...

Since x is in between -2 and -1 but can also equal them :
`-2\leq x\leq -1\\`

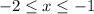
Since y is in between -2 and 2 but can also equal them :
`-2\leq y\leq 2`

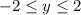
Since the 2 domains don't match, this relation is a function

Hope I helped! :)

Answer 2

Domain : -2≤x≤-1

Range : -2≤y≤2

The relation is a function.

Explanation:

To find the domain and range, first find two points of the graph.

We can find (-2,-2) and (-1,2). Then, make an inequality using the first and second "x-value". It will be -2≤x≤-1.

To find the range, do the same thing. Make an inequality using the first and second "y-value". It will be -2≤y≤2.

To find if the graph is a function, you can do the vertical line test. Basically, you have to see if each vertical line intersects the graph more than once. If it does, it is not a function. If it doesn't, it is a function.