Question

Select the correct answer.

What is the factored form of 1,458x3 − 2?

A.
2(9x − 1)(81x2 + 9x + 1)
B.
2(9x + 1)(81x2 − 9x + 1)
C.
(9x − 2)(81x2 + 18x + 4)
D.
(9x + 2)(81x2 − 18x + 4)

Answer 1

`\huge \boxed{\mathbb{QUESTION} \downarrow}`

What is the factored form of 1,458x³ − 2?

A. 2(9x − 1)(81x² + 9x + 1)

B. 2(9x + 1)(81x² − 9x + 1)

C. (9x − 2)(81x² + 18x + 4)

D. (9x + 2)(81x² − 18x + 4)

`\large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}`

`\sf \: 1458 x ^ { 3 } - 2`

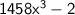
Factor out 2 (common factor).

`\sf \: 2\left(729x^(3)-1\right)`

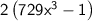
Consider
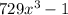`729x^(3)-1`. Rewrite
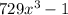`729x^(3)-1` as
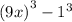`\left(9x\right)^(3)-1^(3)`. The difference of cubes can be factored using the rule:
`a^(3)-b^(3)=\left(a-b\right)\left(a^(2)+ab+b^(2)\right)`.

`\sf\left(9x-1\right)\left(81x^(2)+9x+1\right)`

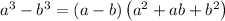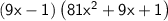
Rewrite the complete factored expression. Polynomial 81x²+9x+1 is not factored as it does not have any rational roots.

`\boxed{ \boxed{ \bf A) \: \: 2\left(9x-1\right)\left(81x^(2)+9x+1\right) }}`