Final answer:
To calculate the change in momentum for a 1,600 kg car that goes from 20 m/s to 0 m/s, use the momentum change formula, resulting in a change in momentum of -32,000 kg m/s.
Step-by-step explanation:
The question asks about the change in momentum of a car that decreases its velocity from 20 m/s to 0 m/s.
To find this change in momentum, we can use the formula
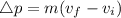 , where Δp is the change in momentum, m is the mass of the car,
, where Δp is the change in momentum, m is the mass of the car,
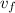 is the final velocity, and
is the final velocity, and
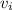 is the initial velocity.
is the initial velocity.
In this case, the car has a mass of 1,600 kg, an initial velocity of 20 m/s, and a final velocity of 0 m/s.
Plugging in these values, we get Δp = 1,600 kg x (0 m/s - 20 m/s)
= -32,000 kg m/s.
The negative sign indicates that the momentum has decreased.