Answer:
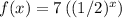 .
.
Explanation:
An exponential function is typically in the form
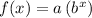 , where
, where
 and
and
 (
(
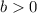 ) are constants to be found.
) are constants to be found.
In this question:
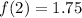 means that
means that
 .
.
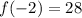 means that
means that
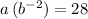 .
.
Divide one of the two equations by the other to eliminate
 and solve for
and solve for
 .
.
The number of the right-hand side of the second equation is larger than that of the first equation. Hence, divide the second equation with the first:
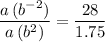 .
.
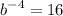 .
.
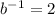 .
.
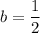 .
.
Substitute
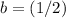 back into either equation (for example, the first equation) and solve for
back into either equation (for example, the first equation) and solve for
 :
:
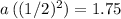 .
.
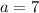 .
.
Substitute
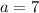 and
and
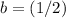 into the other equation. That equation should also be satisfied.
into the other equation. That equation should also be satisfied.
Therefore, this function would be:
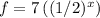 .
.