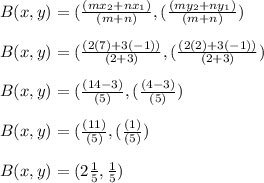The coordinates of point B on AC such that the ratio of AB to BC is 2:3 are: A.
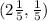 .
.
In this scenario, line ratio would be used to determine the coordinates of the point B on the directed line segment AB that partitions the segment into a ratio of 2 to 3.
In Mathematics and EuclideanGeometry, line ratio can be used to determine the coordinates of a point and this is modeled by this mathematical equation:
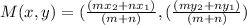
By substituting the given points (-1, -1) and (7, 2) into the formula for line ratio, we have;