Question

22. Find the value of term 2,4

in the sequence.
6, 5, 4, 3, 2,...
O
-7
-6

Answer 1

-7

Explanation:

We are given the following sequence:

`\displaystyle \large{6,5,4,3,2,...}`

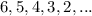
Checking if the sequence is arithmetic by using the following formula:

`\displaystyle \large{a_(n + 1) - a_n = d}`

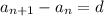
where d is a common difference. Common Difference means that these sequences must have same difference.

Let's check!

5-6 = -1

4-5 = -1

3-4 = -1

2-3 = -1

Since they are the same, the sequence is arithmetic.

General Term of Arithmetic Sequence

`\displaystyle \large{a_n = a_1 + (n - 1)d}`

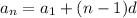
We know that a1 is 6 since 6 is the first term.

d is -1.

Our goal is to find a14. Therefore,

`\displaystyle \large{a_(14) = 6 + (14 - 1)( - 1)} \\ \displaystyle \large{a_(14) = 6 + (13)( - 1)} \\ \displaystyle \large{a_(14) = 6 - 13} \\ \displaystyle \large{a_(14) = - 7}`

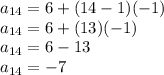
Therefore, the 14th term of sequence is -7.