Question

| 7 + m | - 4 > 8

A. m > -2 or m < -20

B. m > 7 or m < 0

C. m > 5 or m < -19

D. m > 9 or m < -15

Answer 1

m > 5 or m < -19

Explanation:

We are given the Inequality:

`\displaystyle \large - 4 > 8`

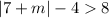
First, add both sides by 4.

`\displaystyle \large - 4 + 4 > 8 + 4 \\ \displaystyle \large`

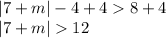
Absolute Value Property

`\displaystyle \large{ |a| = \sqrt{ {a}^(2) } }`

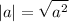
Given a = any expressions and b = any positive numbers, zero or any expressions.

`\displaystyle \largea`

From the Inequality, change > to equal

`\displaystyle \large{ 7 + m = \pm12}`

Subtract 7 both sides.

`\displaystyle \large{ 7 - 7 + m = \pm12 - 7} \\ \displaystyle \large{ m = \pm12 - 7}`

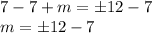
±12-7 can be 12-7 = 5 or -12-7 = -19

`\displaystyle \large{ m = 5, - 19}`

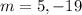
Refer to the attachment. The region is when the absolute value function is greater than constant function y = 12 or a blue horizontal line.

Since the absolute graph is above constant graph when x > 5 and x <-19.

Therefore,

`\displaystyle \large{ m > 5, m < - 19}`