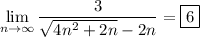Answer:
6
Explanation:
we would like to compute the following limit of a sequence below:
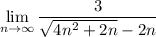
before we do so,here some formulas below which is required:
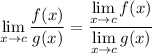
finding the limit:
utilize the first formula:
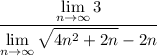
finding the limit of numerator:
Any limit of a constant is equal to the constant therefore the limit of the numerator is equal to 3
finding the limit of the denominator:
rationalize it:
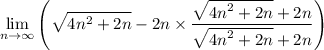
simplify multiplication:
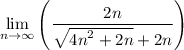
remember that,for limits to infinity, terms less than the highest degree of the numerator or denominator can be disregarded thus we can drop 2n of the square root expression
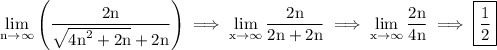
since we've figured out the limit of the both numerator and denominator therefore substitute:
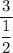
simplify complex fraction:
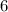
hence,