Question

Evaluate the limit of sequence below:


`\displaystyle \large{\lim_(n \to \infty) (3)/(√(4n^2+2n)-2n)}`
I've been getting 0 as answer. I plotted the graph and it shown that it was approaching 6 when n tends to infinity, but I couldn't figure out how to evaluate the limit like this.
Please show your work on how the answer is 6. Thank you!​

Answer 1

6

Explanation:

we would like to compute the following limit of a sequence below:

`\displaystyle\lim_(n \to \infty) (3)/(√(4n^2+2n)-2n)`

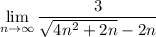
before we do so,here some formulas below which is required:

1. 
   `\displaystyle \lim _(x \to c) (f(x))/(g(x)) = ( \displaystyle \lim _(x \to c)f(x) )/(\displaystyle \lim _(x \to c)g(x) )`

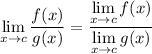
finding the limit:

utilize the first formula:

`( \displaystyle\lim_(n \to \infty)3)/( \displaystyle\lim_(n \to \infty)√(4n^2+2n)-2n)`

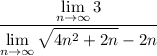
finding the limit of numerator:

Any limit of a constant is equal to the constant therefore the limit of the numerator is equal to 3

finding the limit of the denominator:

rationalize it:

`\displaystyle\lim_(n \to \infty) \left(√(4n^2+2n)-2n * \frac{ \sqrt{ {4n}^(2) + 2n } + 2n}{ \sqrt{{4n}^(2) + 2n } + 2n } \right)`

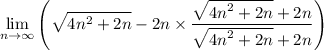
simplify multiplication:

`\displaystyle\lim_(n \to \infty) \left( \frac{ 2n}{ \sqrt{{4n}^(2) + 2n } +2n} \right)`

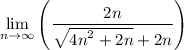
remember that,for limits to infinity, terms less than the highest degree of the numerator or denominator can be disregarded thus we can drop 2n of the square root expression

`\rm\displaystyle\lim_(n \to \infty) \left( \frac{ 2n}{ \sqrt{{4n}^(2) + 2n } + 2n} \right) \implies \lim_(x\to \infty) (2n)/(2n+2n) \implies \lim_(x\to \infty)(2n)/(4n)\implies\boxed{(1)/(2)}`

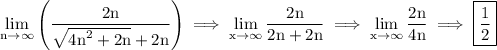
since we've figured out the limit of the both numerator and denominator therefore substitute:

`(3)/( (1)/(2) )`

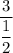
simplify complex fraction:

`6`

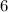
hence,

`\displaystyle\lim_(n \to \infty) (3)/(√(4n^2+2n)-2n)=\boxed{6}`