Answer:
Part A
Cone

(where r is the radius and h is the height)
Given:
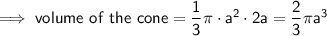
Hemisphere

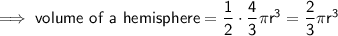
Given

Therefore
volume of cone with radius a = volume of hemisphere with radius a
Part B
![6.82^2*\sqrt[3]{0.005}](https://img.qammunity.org/2023/formulas/mathematics/college/qgw6rkh79wg4svgfea723rrwxx75km1ri5.png)
Take log of base 10:
![\implies \log_(10)(6.82^2*\sqrt[3]{0.005})](https://img.qammunity.org/2023/formulas/mathematics/college/zij40bu7q96xpjprdpi9hcyix5g2hhyw7q.png)
Using log law
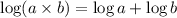 :
:
![\implies \log_(10)(6.82^2)+\log_(10)(\sqrt[3]{0.005})](https://img.qammunity.org/2023/formulas/mathematics/college/28d6z4e54y18d4t79p9ci35p3bey6i1lmh.png)
Using low law
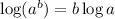
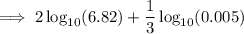
Log tables
The characteristic of the logarithm of a number is the exponent of 10 in its scientific notation.
The mantissa is found using the log tables and is always prefixed by a decimal point.
The row is the first two non-zero digits of the number, and the column is the 3rd digit of the number
Use the log tables to find
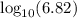 :
:
6.82 = 6.82 × 10⁰
⇒ characteristic = 0
log table: row 68, column 2 ⇒ mantissa 8338 ⇒ 0.8338
characteristic + mantissa = 0 + 0.8338 = 0.8338
Therefore,
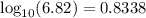
Use the log tables to find
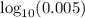 :
:
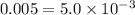
⇒ characteristic = -3
log table: row 50, column 0 ⇒ mantissa 6990 ⇒ 0.6990
characteristic + mantissa = -3 + 0.6990 = -2.301
Therefore,
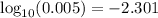
Therefore,
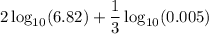
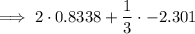
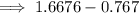
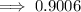
Therefore,
![\log_(10)(6.82^2*\sqrt[3]{0.005})=0.9006](https://img.qammunity.org/2023/formulas/mathematics/college/ix632adv9i8jw5o9vdulkzksajlby89vv3.png)
Using
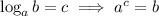
![\implies 6.82^2*\sqrt[3]{0.005}=10^(0.9006)](https://img.qammunity.org/2023/formulas/mathematics/college/zj2nyouil2257knpoa3xx580cyjzu02we1.png)
![\implies 6.82^2*\sqrt[3]{0.005}=7.954](https://img.qammunity.org/2023/formulas/mathematics/college/vrmmnswuzlweck3idjw4lcwiqah1w5bfcj.png)