Answer:
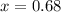
Explanation:
We would like to find out the value of x using logarithms of the given equation .The equation is ,
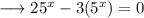
Add
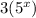 on both sides,
on both sides,
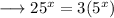
Using log to the base 10 on both sides, we have;
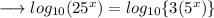
Recall that
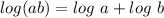 .
.
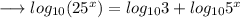
Recall the properties of logarithm as
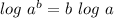 .
.
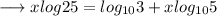
Again we can rewrite it as ,
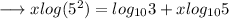
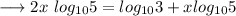
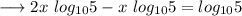
Simplify,
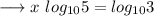
Divide both sides by log5 ,
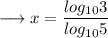
Put on the values of log 3 and log5 ,
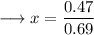
Simplify,

And we are done!