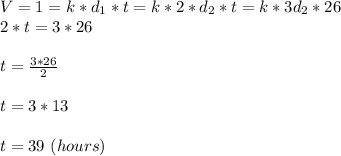Answer:
Explanation:
Let's say
d1 the outflow of the first pump
d2 the outflow of the second pump
V=1 is the volume of the tank
Since the second pump takes twice as long as the first to fill the tank,
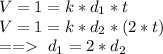
Two pumps can fill a pool tank in 26 hours when working together:
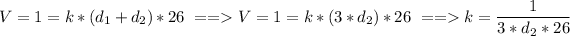
How long does it take the first pump alone to fill the tank: