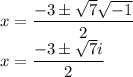Answer:

Explanation:
We are given the equation:
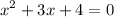
Since the expression is not factorable with real numbers, we use the Quadratic Formula.
Quadratic Formula
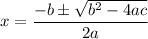
Compare the expression:
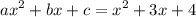
a = 1
b = 3
c = 4
Substitute a = 1, b = 3 and c = 4 in the formula.
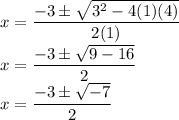
Imaginary Unit
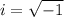
Therefore,