Question

Given that the following two geometric series(meetkundige reekse) are covergent 1+x+x²+x³+... And 1-x+x²-x³+... Determine the value(s) of x for witch the sum of the following two series is equel​

Answer 1

x = 0

Explanation:

Given:

`\displaystyle \large{S = 1+x+x^2+x^3+... \to (1)}\\\displaystyle \large{S=1-x+x^2-x^3+... \to (2)}`

• Both sum are convergent.

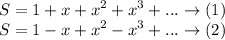
Convergent Definition / Infinite Geometric Series:

`\displaystyle \large{S=(a_1)/(1-r) \ \ \ttr}`

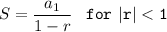
• S = sum
• 
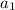  `\displaystyle \large{a_1}` = first term
• r = common ratio

From (1):-

Our common ratio is x and first term is 1:

`\displaystyle \large{S=(1)/(1-x)}`

From (2):-

Our common ratio is -x and first term is 1:

`\displaystyle \large{S=(1)/(1+x)}`

To find:

• x-value(s) that make both series equal to each other.

So we solve the equation between two series:

`\displaystyle \large{(1)/(1-x)=(1)/(1+x)}`

|x| < 1 since it’s convergent so |x| cannot be greater than 1 or less than -1.

Solve the equation:

`\displaystyle \large{(1)/(1-x)(1+x)(1-x) = (1)/(1+x)(1-x)(1+x)}\\\displaystyle \large{1(1+x)=1(1-x)}\\\displaystyle \large{1+x=1-x}\\\displaystyle \large{2x=0}\\\displaystyle \large{x=0}`

Therefore, the only possible x-value for both convergent sum to be equal is x = 0