Question

Find the ‘exact’ perimeter of each triangle

Answer 1

`\huge\boxed{\sf 8 + 4√(2) \ cm }`

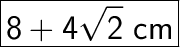
Explanation:

`\theta = 45 \textdegree`

opposite = 4 cm

Using tan first to find the adjacent side:

`\displaystyle tan \theta = (opposite)/(adjacent) \\\\tan \ 45 = (4)/(adjacent)\\\\1 = (4)/(adjacent) \\\\Multiply \ 'adjacent' \ to \ both \ sides\\\\adjacent = 4 \ cm`

Finding Hypotenuse now by using Pythagorean theorem:

`(Hyp)^2 = (base)^2 + (perp)^2`

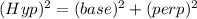
where base = 4, hyp = 4

(Hyp)² = (4)² + (4)²

(Hyp)² = 16 + 16

(Hyp)² = 32

Take sqrt on both sides

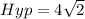`Hyp = 4√(2)` cm

Exact perimeter of triangle:

= base + perpendicular + hypotenuse

= 4 + 4 + 4√2

=
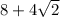`8 + 4√(2)` cm

`\rule[225]{225}{2}`