Question

10. Use synthetic division to completely factor y = x3 - 4x2 - 9x + 36 by x + 3.

O.
y = (x + 3)(x - 4)(x - 3)
y = (x + 3)(x - 4)(x + 3)
y = (x + 3)(x + 4)(x - 3)
y = (x + 3)(x + 4)(x + 3)

Answer 1

Start with,

`(x^3-4x^2-9x+36)/(x+3)`

Look at first terms,
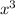`x^3` and
`x` in divisor, with what do you have to multiply
`x` so that you end up with
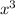`x^3`? The answer is
`x^2`.

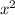So you write,

`(x^3-4x^2-9x+36)/(x+3)=x^2`

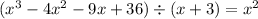
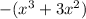`-(x^3+3x^2)` (because you are subtracting
`x^2(x+3)`.

Which becomes when u subtract columns,

`(-7x^2-9x+36)/(x+3)=x^2`

Now repeat the procedure,

`(-7x^2-9x+36)/(x+3)=x^2-7x`

`-(-7x^2-21x)`

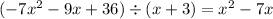
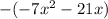
which becomes

`(12x+36)/(x+3)=x^2-7x`

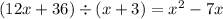
And again,

`(12x+36)/(x+3)=x^2-7x+12`

`-(12x+36)`

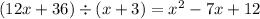
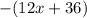
becomes,

`0=x^2-7x+12`

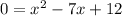
Since the RHS is 0 that means
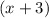`(x+3)` is a factor.

Now you can factor
`x^2-7x+12=(x-4)(x-3)` because
`-4\cdot-3=12` and
`-4+(-3)=-7`.

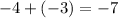Combine the factors and get
`(x+3)(x-4)(x-3)`.

Hope this helps :)

Answer 2

Answer: A

Explanation:

`P(x)= x^3 - 4x^2 - 9x + 36 \\D(x)=x + 3\\\\\begin{array}&x^3&x^2&x&1\\---&---&---&---&---\\&1&-4&-9&36\\x=-3&&-3&21&-36\\---&---&---&---&---\\&1&-7&12&0\\\end{array}\\\\\\P(x)= x^3 - 4x^2 - 9x + 36 \\=(x+3)(x^2-7x+12)\\=(x+3)(x^2-3x-4x+12)\\=(x+3)(x(x-3)-4(x-3))\\=(x+3)(x-3)(x-4)\\\\Answer \ A`