Find all real solutions Tan pi/3 x-3=0

Question

asked Nov 28, 2023 63.0k views

1 Answer

Ivan Poliakov · Answer 1 · 2023-12-01T20:09:01+0000

Explanation:

If the question is like this,

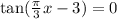
$\tan( (\pi)/(3)x - 3 ) = 0$

We take the arc tan of both sides.

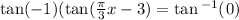
$\tan( - 1) ( \tan( (\pi)/(3)x - 3 ) = \tan {}^( - 1) ( {}^( )0 )$

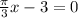
$(\pi)/(3) x - 3 = 0$

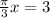
$(\pi)/(3) x = 3$

$= (9)/(\pi)$

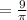
Since the period of a tan function, is pi, we divide pi by pi/3 since pi/3is the coeffeicent of the x variable

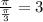
$(\pi)/( (\pi)/(3) ) = 3$

So the answer is

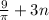
$(9)/(\pi) + 3n$

If this the question,

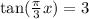
$\tan( (\pi)/(3) x) = 3$

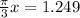
$(\pi)/(3) x = 1.249$

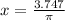
$x = (3.747)/(\pi)$

The period is once again 3 so we have

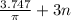
$(3.747)/(\pi) + 3n$

where n is a interger.