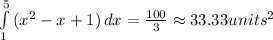Answer:
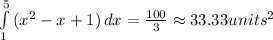
Explanation:
To determine the area of the definite integral, we take each term and find its corresponding integral. We know that
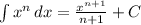 , so therefore we rewrite the expression as
, so therefore we rewrite the expression as
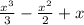 .
.
Now, we plug in each limit into the expression and find the difference between them:
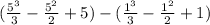
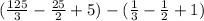
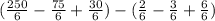
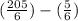
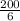
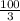
Therefore,