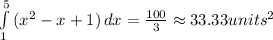Question

18. Use limits to find the area between the graph of the function and the x axis given by the definite integral. ∫_1^5·(x^2-x+1)dx

Answer 1

`\int\limits^5_1 {(x^2-x+1)} \, dx= (100)/(3)\approx33.33units^2`

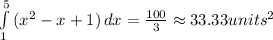
Explanation:

To determine the area of the definite integral, we take each term and find its corresponding integral. We know that
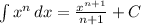`\int\limits {x^n} \, dx =(x^(n+1))/(n+1) +C`, so therefore we rewrite the expression as
`(x^3)/(3)-(x^2)/(2)+x`.

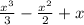Now, we plug in each limit into the expression and find the difference between them:

`((5^3)/(3)-(5^2)/(2)+5)-((1^3)/(3)-(1^2)/(2)+1)`

`((125)/(3)-(25)/(2)+5)-((1)/(3)-(1)/(2)+1)`

`((250)/(6)-(75)/(6)+(30)/(6) )-((2)/(6)-(3)/(6)+(6)/(6))`

`((205)/(6))-((5)/(6))`

`(200)/(6)`

`(100)/(3)`

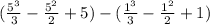
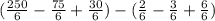
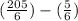
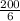
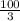
Therefore,
`\int\limits^5_1 {(x^2-x+1)} \, dx= (100)/(3)\approx33.33units^2`