By definition of absolute value, you have

or more simply,
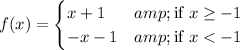
On their own, each piece is differentiable over their respective domains, except at the point where they split off.
For x > -1, we have
(x + 1)' = 1
while for x < -1,
(-x - 1)' = -1
More concisely,
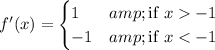
Note the strict inequalities in the definition of f '(x).
In order for f(x) to be differentiable at x = -1, the derivative f '(x) must be continuous at x = -1. But this is not the case, because the limits from either side of x = -1 for the derivative do not match:
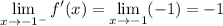
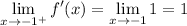
All this to say that f(x) is differentiable everywhere on its domain, except at the point x = -1.