Question

Factor completely.

`x^(8)-(1)/(81)`

Answer 1

We have 3⁴ = 81, so we can factorize this as a difference of squares twice:

`x^8 - \frac1{81} = \left(x^2\right)^4 - \left(\frac13\right)^4 \\\\ x^8 - \frac1{81} = \left(\left(x^2\right)^2 - \left(\frac13\right)^2\right) \left(\left(x^2\right)^2 + \left(\frac13\right)^2\right) \\\\ x^8 - \frac1{81} = \left(x^2 - \frac13\right) \left(x^2 + \frac13\right) \left(\left(x^2\right)^2 + \left(\frac13\right)^2\right) \\\\ x^8 - \frac1{81} = \left(x^2 - \frac13\right) \left(x^2 + \frac13\right) \left(x^4 + \frac19\right)`

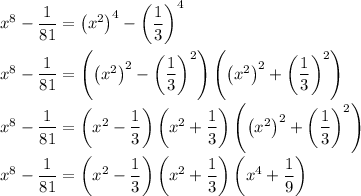
Depending on the precise definition of "completely" in this context, you can go a bit further and factorize
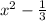`x^2-\frac13` as yet another difference of squares:

`x^2 - \frac13 = x^2 - \left(\frac1{\sqrt3}\right)^2 = \left(x-\frac1{\sqrt3}\right)\left(x+\frac1{\sqrt3}\right)`

And if you're working over the field of complex numbers, you can go even further. For instance,

`x^4 + \frac19 = \left(x^2\right)^2 - \left(i\frac13\right)^2 = \left(x^2 - i\frac13\right) \left(x^2 + i\frac13\right)`

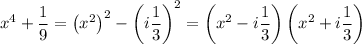
But I think you'd be fine stopping at the first result,

`x^8 - \frac1{81} = \boxed{\left(x^2 - \frac13\right) \left(x^2 + \frac13\right) \left(x^4 + \frac19\right)}`