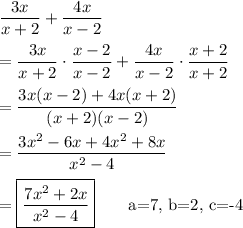Question

I need help please. I don't understand and I need this to graduate​

Answer 1

Hope this one helps

Answer 2

(a, b, c) = (7, 2, -4)

Explanation:

The fractions are added in the usual way, and the result simplified. That involves finding a common denominator, and expressing each fraction in terms of it.

Here the denominators have no factors in common, so the common denominator is their product. That common denominator is the difference of squares, a "special product."

`(3x)/(x+2)+(4x)/(x-2)\\\\=(3x)/(x+2)\cdot(x-2)/(x-2)+(4x)/(x-2)\cdot(x+2)/(x+2)\\\\=(3x(x-2)+4x(x+2))/((x+2)(x-2))\\\\=(3x^2-6x+4x^2+8x)/(x^2-4)\\\\=\boxed{(7x^2+2x)/(x^2-4)}\qquad\text{a=7, b=2, c=-4}`