The points (0, 0) and (1, 2) on the graph represent the cost-slices relationship, where (0, 0) signifies zero cost for zero slices, and (1, 2) denotes a cost of 2 units for 1 slice of pizza.
The given points (0, 0) and (1, 2) are coordinates on the graph, representing the relationship between the number of slices of pizza and the cost per slice. In the context of the problem, the x-coordinate typically corresponds to the number of slices, and the y-coordinate represents the cost. Therefore, (0, 0) indicates that when there are zero slices of pizza (x = 0), the cost is zero (y = 0). This is a logical starting point, suggesting that there is no cost associated with zero slices.
Similarly, the point (1, 2) implies that for 1 slice of pizza (x = 1), the cost is 2 units (y = 2). This suggests a proportional relationship, indicating that each additional slice incurs an additional cost. The slope between these two points is calculated as ,
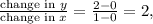 confirming the proportional nature of the relationship.
confirming the proportional nature of the relationship.
Understanding the interpretation of these points in the context of the problem and calculating the slope reinforces the idea that the cost per slice of pizza is proportional to the number of slices. The points on the graph provide a clear visual representation of this relationship, offering insights into the cost dynamics associated with varying quantities of pizza slices.