a. What can you use to find the height of the pole?
solution: We can use Pythagoras theorem to find the height of the pole.
b. Write and solve a quadratic equation to find the height of the pole.
solution:
a² + b² = c²
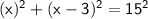
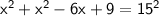
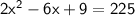
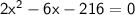
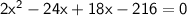
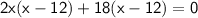
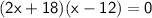
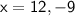
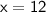
height of the pole: 12 ft
c. How far is the hook from the base of the pole?
solution: (x-3) → (12-3) → 9