
- Revathi's age is 1/3 of her mother's age. If their difference in age is 24 years, find Revathi's age.
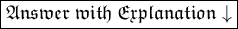
Given,
- Mother's age = x
- Revathi's age = 1/3 x = ?
- Difference in their age = 24 years ⇨ x - 1/3 x = 24.
Now, let's solve this question using the above equation which we just formed.
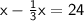
Combine x and
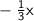 to get
to get
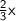 .
.
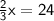
Multiply both sides by
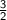 , the reciprocal of
, the reciprocal of
 .
.
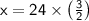
Express
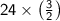 as a single fraction.
as a single fraction.
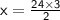
Multiply 24 and 3 to get 72.
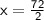
Divide 72 by 2 to get 36.
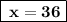
We now have the age of Revathi's mother (x) = 36 years. Now, let's find Revathi's age ⇨
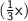
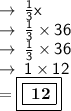
- So, Revathi is 12 years old.