What you're really doing is finding the slope of the line between two points you need to calculate.
Because a=3, you're told that one point will always be (3, f(3)).
The second point will be (3+h, f(3+h)).
For the first point, f(3) = 7/3, so your first point is always (3, 7/3).
For h=1
The x-value of your second point is a+h, or 3+1 = 4 in this case.
f(4) = 7/4.
So the average rate of change, aka the slope of the line between (3, 7/3) and (4, 7/4), is the usual slope formula:
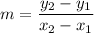
In this h=1 situation, that becomes:
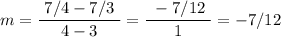
You're repeat this process for each new h-value.