Question

Help meeee. Im in calculus and I need this done by tonight and I keep messing something up

Answer 1

What you're really doing is finding the slope of the line between two points you need to calculate.

Because a=3, you're told that one point will always be (3, f(3)).

The second point will be (3+h, f(3+h)).

For the first point, f(3) = 7/3, so your first point is always (3, 7/3).

For h=1

The x-value of your second point is a+h, or 3+1 = 4 in this case.

f(4) = 7/4.

So the average rate of change, aka the slope of the line between (3, 7/3) and (4, 7/4), is the usual slope formula:

`m=(y_2-y_1)/(x_2 - x_1)`

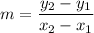
In this h=1 situation, that becomes:

`m=(~7/4-7/3~)/(4 - 3) = (~-7/12~)/(1) = -7/12`

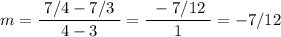
You're repeat this process for each new h-value.