Answer:
Vertex:
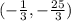
Y-intercept:

Explanation:
The x-coordinate of the vertex would be
 and the y-coordinate of the vertex is whatever the output is given the value of x.
and the y-coordinate of the vertex is whatever the output is given the value of x.
Therefore, the x-coordinate of the vertex is
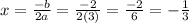
This means the y-coordinate of the vertex is

So, the vertex is
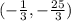
The y-intercept of a function is the y-value at which x=0, or the y-value when the function crosses the y-axis. Therefore, if we plug x=0 into the function, we see that
 , so our y-intercept is -8 or (0,-8).
, so our y-intercept is -8 or (0,-8).
I attached a graph below to help you visualize the vertex and y-intercept given the function.