Answer:
h = 1053 ft (to the nearest foot)
Explanation:
The sum of the interior angles of a triangle is 180°
Therefore, the angle at the bottom vertex of the triangle is:
180 - 69.2 - 65.5 = 45.3°
Sine rule:
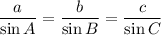
where A, B and C are the angles in a triangle, and a, b and c are the sides opposite those angles (e.g. side a is opposite angle A).
Now we can use the sine rule to calculate the length of the diagonal sides of the triangle.
Let a = the length of the right diagonal (the side with unknown length adjacent to angle 65.5°)
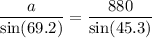
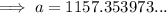
Now we can use the sine trig ratio to determine h:
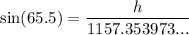
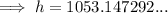
Therefore, h = 1053 ft (to the nearest foot)