Answer:
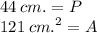
Step-by-step Step-by-step explanation:
All angles and edges are congruent in a square, so first, find the total boundary by multiplying the length of the edge by 4:
![\displaystyle 4l = P \\ 4[11] = P \\ \\ 44 = P](https://img.qammunity.org/2023/formulas/mathematics/high-school/ay9j31c2o8c1c47b415420ukmrn57z19gj.png)
Now, for the area, you square the length of the edge:

I am joyous to assist you at any time.