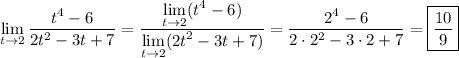Question

Lim t^4 - 6 / 2t^2 - 3t + 7

x→2
Evaluate the limit using the appropriate Limit Law(s). (If an answer does not exist, enter DNE.)

I am stuggling with finding the answer. Please helpppp. Thank you.

Answer 1

I think you meant to say

`\displaystyle \lim_(t\to2)(t^4-6)/(2t^2-3t+7)`

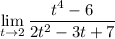
(as opposed to x approaching 2)

Since both the numerator and denominator are continuous at t = 2, the limit of the ratio is equal to a ratio of limits. In other words, the limit operator distributes over the quotient:

`\displaystyle \lim_(t\to2) (t^4 - 6)/(2t^2 - 3t + 7) = (\displaystyle \lim_(t\to2)(t^4-6))/(\displaystyle \lim_(t\to2)(2t^2-3t+7))`

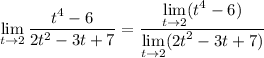
Because these expressions are continuous at t = 2, we can compute the limits by evaluating the limands directly at 2:

`\displaystyle \lim_(t\to2) (t^4 - 6)/(2t^2 - 3t + 7) = (\displaystyle \lim_(t\to2)(t^4-6))/(\displaystyle \lim_(t\to2)(2t^2-3t+7)) = (2^4-6)/(2\cdot2^2-3\cdot2+7) = \boxed{\frac{10}9}`