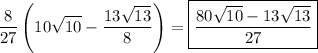First, rewrite the equation so that y is a function of x :

(If you were to plot the actual curve, you would have both
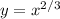 and
and
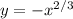 , but one curve is a reflection of the other, so the arc length for 1 ≤ x ≤ 8 would be the same on both curves. It doesn't matter which "half-curve" you choose to work with.)
, but one curve is a reflection of the other, so the arc length for 1 ≤ x ≤ 8 would be the same on both curves. It doesn't matter which "half-curve" you choose to work with.)
The arc length is then given by the definite integral,
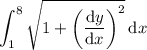
We have
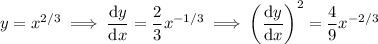
Then in the integral,
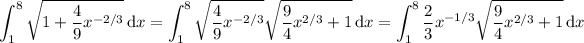
Substitute
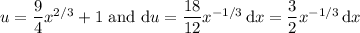
This transforms the integral to
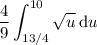
and computing it is trivial:
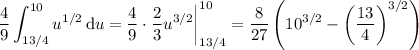
We can simplify this further to