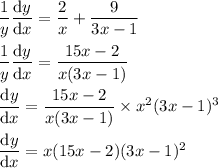Use the power, product, and chain rules:
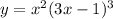
• product rule
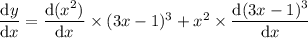
• power rule for the first term, and power/chain rules for the second term:
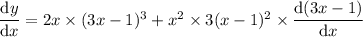
• power rule
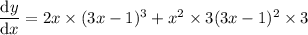
Now simplify.
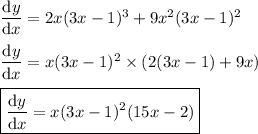
You could also use logarithmic differentiation, which involves taking logarithms of both sides and differentiating with the chain rule.
On the right side, the logarithm of a product can be expanded as a sum of logarithms. Then use other properties of logarithms to simplify
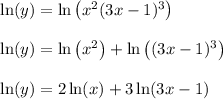
Differentiate both sides and you end up with the same derivative: