Question

NEED HELP ASAP! Which of the following could be the second equation in the system of equations seen below, so that the system has infinite solutions? Select all that apply.

​

Answer 1

B, E, F

Explanation:

If the system has infinite solutions, then the 2 equations will be identical.

So we are looking for an equation, which, when simplified or rearranged or multiplied by a constant, will be the same as the given equation
`4x-6y=12`

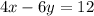
If we multiply equation A by 2 we get: 4x + 6y = 12

This is not the same as the original equation since the operation sign is addition rather than subtraction.

If we divide equation B by 5 we get: 4x - 6y = 12

This is identical to the original equation, and therefore could be the second equation.

Equation C: y = (2/3)x + 12

Multiply by 3: 3y = 2x + 36

Multiply by 2: 6y = 4x + 72

Rearrange: 4x - 6y = -72

If we divide equation D by 1.5 we get: 4x - (8/3)y = 8

Equation E: y = (2/3)x - 2

Multiply by 3: 3y = 2x - 6

Multiply by 2: 6y = 4x - 12

Rearrange: 4x - 6y = 12

This is identical to the original equation, and therefore could be the second equation.

Equation F: 3y = 2x - 6

Multiply by 2: 6y = 4x - 12

Rearrange: 4x - 6y = 12

This is identical to the original equation, and therefore could be the second equation.