Answer:
229
Step-by-step explanation:
Here we are given a polynomial p(x) and we need to find the remainder when it is divided by (x-4) . As we know that if a polynomial, say
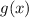 is divided by
is divided by
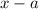 then the remainder is
then the remainder is
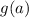 .
.
Firstly equate
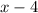 with 0 , we have;
with 0 , we have;

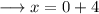
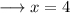
Now substitute
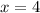 in
in
 ,
,
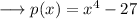
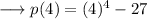
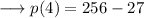

Hence the remainder is 229 .