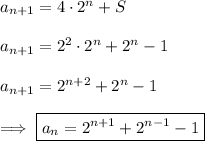From the given recurrence, it follows that
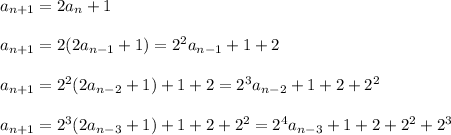
and so on down to the first term,
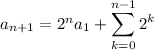
(Notice how the exponent on the 2 and the subscript of a in the first term add up to n + 1.)
Denote the remaining sum by S ; then
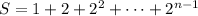
Multiply both sides by 2 :
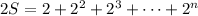
Subtract 2S from S to get
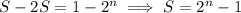
So, we end up with