Hєℓℓσ Tнєяє !
¶ Cσncєptѕ tσ вє uѕєd hєrє :
✦ Degree of a polynomial íѕ thє híghєѕt pσwєr σf α vαríαвlє ín thє gívєn pσlчnσmíαl.
✦ numвєr σf tєrmѕ = díѕtínguíѕhєd tєrmѕ ín α pσlчnσmíαl hαvíng díffєrєnt єхpσnєntíαl pσwєr, αnd ѕєpєrαtєd вч mαthєmαtícαl σpєrαtσrѕ ( + αnd - )
➳ nσtє :
#1. Combine the like terms before performing any operation.
#2. íf thєrє íѕ α multíplícαtíσn σr dívíѕíσn σpєrαtσr ín thє pσlчnσmíαl, wє hαvє tσ fínd thє prσduct fírѕt tσ pєrfσrm αnч σthєr σpєrαtíσn.
✿ lєt'ѕ prσcєєd ~
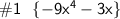
![\rule{20cm}{1 mm}]()
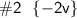
![\rule{20cm}{1 mm}]()
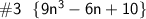
![\rule{20cm}{1 mm}]()
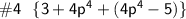
[ cσmвínє thє líkє tєrmѕ ]
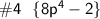
![\rule{20cm}{1 mm}]()
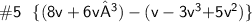
[ cσmвínє thє líkє tєrmѕ ]
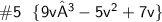
![\rule{20cm}{1 mm}]()
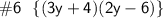
[ pєrfσrm thє multíplícαtíσn ]
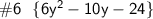
![\rule{20cm}{1 mm}]()
Keep learning ~