Answer:
The interior angle would measure
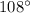 . Assuming that this polygon is regular, it would contain
. Assuming that this polygon is regular, it would contain
 sides.
sides.
Explanation:
An exterior angle in a polygon is supplementary with the interior angle that shares the same vertex with the exterior angle. In other words, the sum of these two angles would be
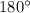 .
.
In this question, the exterior angle measures
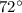 . Therefore, the interior angle that shares the same vertex with this
. Therefore, the interior angle that shares the same vertex with this
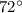 exterior angle would measure
exterior angle would measure
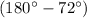 , which is
, which is
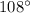 .
.
The sum of all interior angles in a polygon with
 sides (regular or not) is
sides (regular or not) is
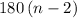 degrees.
degrees.
All the interior angles in a regular polygon are equal. Hence, in a regular polygon with
 sides (and hence
sides (and hence
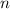 vertices,) each of the
vertices,) each of the
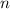 interior angles would measure
interior angles would measure
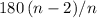 degrees.
degrees.
Assume that the polygon in this question is regular. Again, let
 be the number of sides in this polygon. Each interior angle would measure
be the number of sides in this polygon. Each interior angle would measure
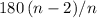 degrees. However, it was also deduced that an interior angle of this polygon measures
degrees. However, it was also deduced that an interior angle of this polygon measures
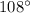 . That is:
. That is:
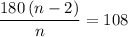 .
.
Solve for
 :
:
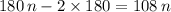 .
.
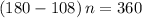 .
.
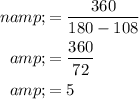 .
.
In other words, if this polygon is regular, it would contain
 sides.
sides.