Question

Find the volume of the following solid. Using cylindrical coordinates

z = 4 - 4(x^2 + y^2)

z = (x^2 + y^2)^2 -1

Answer 1

In cylindrical coordinates, the equations of the surfaces become

`z = 4 - 4r^2 \\\\ z = (r^2)^2 - 1 = r^4 - 1`

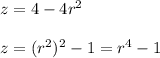
These surfaces intersect on the cylinder of radius 1 with cross sections parallel to the x,y-plane:

`4 - 4r^2 = r^4 - 1 \\\\ \implies r^4 + 4r^2 - 5 = (r-1)(r+1)(r^2+5) = 0 \\\\ \implies r=1`

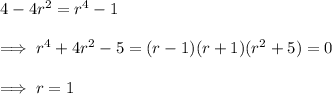
Then in cylindrical coordinates, the volume of the space bounded by these surfaces is

`\displaystyle \int_0^(2\pi)\int_0^1\int_(r^4-1)^(4-4r^2)r\,\mathrm dz\,\mathrm dr\,\mathrm d\theta = 2\pi \int_0^1 \int_(r^4 - 1)^(4-4r^2)r\,\mathrm dz\,\mathrm dr \\\\ = \pi \int_0^1 (4-4r^2)^2 - (r^4-1)^2 \,\mathrm dr \\\\ = \pi \int_0^1 (15-32r^2+18r^4-r^8)\,\mathrm dr = \boxed{(352\pi)/(45)}`