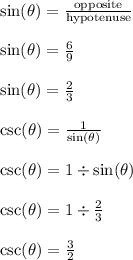Question

I needddddd heelllpppp pleaseeee

Answer 1

Problem 3

Answer: 3/2

=====================================================

Step-by-step explanation:

Use the pythagorean theorem to find the length of the missing side.

`a^2 + b^2 = c^2\\\\a^2 + (3√(5))^2 = 9^2\\\\a^2+3^2*(√(5))^2 = 9^2\\\\a^2 + 9(5) = 81\\\\a^2 + 45 = 81\\\\a^2 = 81-45\\\\a^2 = 36\\\\a = √(36)\\\\a = 6\\\\`

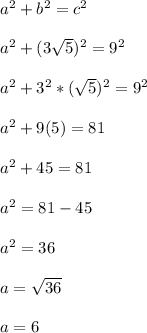
This is the length of the missing vertical side. This side is opposite the angle theta.

`\csc = \text{cosecant}\\\\\csc(\theta) = \frac{\text{hypotenuse}}{\text{opposite}}\\\\\csc(\theta) = (9)/(6)\\\\\csc(\theta) = (3*3)/(3*2)\\\\\csc(\theta) = (3)/(2)\\\\`

Alternatively, you can compute it like this

`\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\\\\\sin(\theta) = (6)/(9)\\\\\sin(\theta) = (2)/(3)\\\\\csc(\theta) = (1)/(\sin(\theta))\\\\\csc(\theta) = 1 / \sin(\theta)\\\\\csc(\theta) = 1 / (2)/(3)\\\\\csc(\theta) = (3)/(2)\\\\`

Answer 2

3/2

Step-by-step explanation:

Csc(theta) = 1/Sin(theta)

So we have to find the side opposite theta.

a = 3*sqrt(5)

b = ?

c = 9

a^2 + b^2 = c^2

(3sqrt(5)) ^2 + b^2 = 9^2

9*5 + b^2 = 81

b^2 = 81 = 45

b^2 = 36

sqrt(b^2) = sqrt(36)

b = 6

Sin(theta) = 6/9

Csc(theta) = 1 / sin(theta) = 9/6

Csc(theta = 3/2