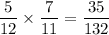Answer:
35/132 = 0.27 (nearest hundredth)
Step-by-step explanation:
Total number of biscuits = 12
Number of digestives = 7
Number of chocolate biscuits = 5
The probability of the first biscuit being a digestive is 7/12
As the first biscuit was not replaced, the total number of biscuits is now 11.
So the probability of the second biscuit being chocolate is 5/11
Therefore, the probability of the first biscuit being a digestive AND the second being chocolate is:
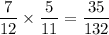
Similarly,
The probability of the first biscuit being chocolate is 5/12
As the first biscuit was not replaced, the total number of biscuits is now 11.
So the probability of the second biscuit being a digestive is 7/11
Therefore, the probability of the first biscuit being chocolate AND the second being a digestive is: