You can either transform this quadratic equation into a vertex form which would rather painful or use derivatives.
I'll use dervatives. We know that vertex of a quadratic function is either its maxima or its minima, since the leading coefficient
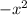 has a negative prefix that means we get a downward turned parabola with minima being the vertex.
has a negative prefix that means we get a downward turned parabola with minima being the vertex.
First we take the derivative with respect to x,
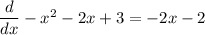
The derivative is esentially information what is the slope of a function at a particular x. When the slope is 0 we reached some sort of turning point, such as minima.
We therefore do,
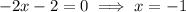
So at
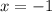 there appears to be a minima or x-coordinate of the vertex of the function.
there appears to be a minima or x-coordinate of the vertex of the function.
Plug the coordinate into the function to get y,
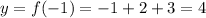
So the vertex of the function is at
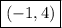 .
.
Assuming you don't know derivatives, there is another way.
First compute the roots of the function,
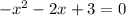

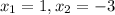
In the middle between
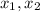 is an x coordinate of a vertex,
is an x coordinate of a vertex,
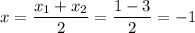
Just like we had before, we compute for y,
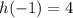 and again the result is
and again the result is
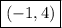 .
.
Hope this helps :)