Answer:

Explanation:
The midpoint is the middle point of a line segment that bisects (splits into 2 equal parts) the line segment. When we calculate the midpoint, we basically find the average of the x-coordinate, then the average of the y-coordinates. The formula is:
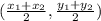
In this formula, (x₁, y₁) and (x₂, y₂) are the endpoints of the segment.
We are given the points (4,5) and (2,2). Match the value and the corresponding variable.
Substitute these values into the formula.
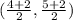
Solve the numerators.
- X-coordinate: 4+2= 6
- Y-coordinate: 5+2=7
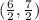
Divide.
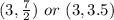
The midpoint of the line segment is (3, 7/2) or (3, 3.5).