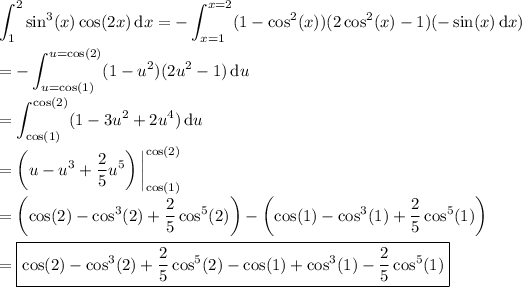Question

Evaluate:


`\int \limits^(2)_(1) { \sin }^(3) x. \cos(2x) dx`
hello, anyone can help me if you don't mind, I am getting confused.
Thanks, I really appreciate​

Answer 1

Recall some identities:

sin²(x) + cos²(x) = 1

cos(2x) = cos²(x) - sin²(x)

and from the first identity, you can establish that

cos(2x) = 2 cos²(x) - 1

So, rewrite the integrand as much as possible in terms of cos(x) :

`\sin^3(x) \cos(2x) = \sin(x) \sin^2(x) (\cos^2(x)-\sin^2(x)) \\\\ \sin^3(x) \cos(2x) = \sin(x) (1-\cos^2(x)) (2\cos^2(x) - 1)`

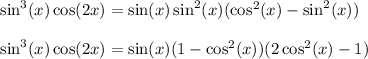
Then in the integral, substitute u = cos(x) and du = -sin(x) dx. With some rewriting, you end up with

`\displaystyle \int_1^2 \sin^3(x) \cos(2x) \,\mathrm dx = -\int_(x=1)^(x=2) (1-\cos^2(x))(2\cos^2(x)-1) (-\sin(x)\,\mathrm dx) \\\\ = -\int_(u=\cos(1))^(u=\cos(2)) (1-u^2)(2u^2-1)\,\mathrm du \\\\ = \int_(\cos(1))^(\cos(2)) (1-3u^2+2u^4) \,\mathrm du \\\\ = \left(u-u^3+\frac25u^5\right)\bigg|_(\cos(1))^(\cos(2)) \\\\ = \left(\cos(2)-\cos^3(2)+\frac25\cos^5(2)\right) - \left(\cos(1)-\cos^3(1)+\frac25\cos^5(1)\right) \\\\ = \boxed{\cos(2) - \cos^3(2) + \frac 25 \cos^5(2) - \cos(1) + \cos^3(1) - \frac25 \cos^5(1)}`