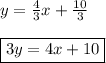Answer:
It is 3y = 4x + 10
Explanation:
Let's first get the slope of the curve.
[ slope is the derivative of the equation ]
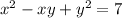
introduce dy/dx :
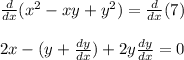
make dy/dx the subject:
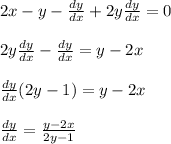
At point (-1, 2):
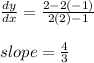
but a tangent has the same slope as the curve:

m is the slope
c is the y-intercept
At (-1, 2):

equation: