Question

You push a shopping cart for fun with a force of 60N. If the shopping cart has a mass of 12kg, what is the acceleration on the cart

Answer 1

`\boxed {\boxed {\sf 5 \ m/s^2 }}`

Step-by-step explanation:

We are asked to find the acceleration of a shopping cart, given the force and mass. According to Newton's Second Law of Motion, force is the product of mass and acceleration.

`F= m * a`

The mass of the shopping cart is 12 kilograms and the force is 60 Newtons. Let's convert the units for force. 1 Newton is equal to 1 kilogram meter per second squared, so the force of 60 Newtons is also 60 kilogram meters per second squared.

• F= 60 kg*m/s²
• m= 12 kg

Substitute the values into the formula.

`60 \ kg *m/s^2 = 12 \ kg * a`

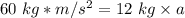
We are solving for the acceleration, so we must isolate the variable a. It is being multiplied by 12 kilograms. The inverse operation of multiplication is division, so we divide both sides by 12 kg.

`\frac {60 \ kg *m/s^2 } { 12 \ kg}= (12 \ kg * a )/(12 \ kg)`

`\frac {60 \ kg *m/s^2 } { 12 \ kg}=a`

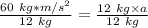
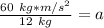
The units of kilograms cancel.

`\frac {60 \ m/s^2 } { 12 }=a`

`5 \ m/s^2 =a`

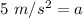
The acceleration of the shopping cart is 5 meters per second squared.