
Let consider the given triangle be ABC
Here, It is given in the question that ,
Therefore,
By using Angle sum property
- It states that the sum of all angles of triangles are equal to 180°
That is,
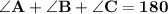
Subsitute the required values,
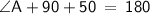
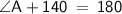
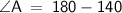
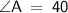
Thus, The angle A is 40°
Now,
We have to find the side a and b
We know that,
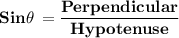
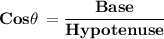
For side A
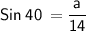
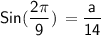
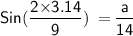
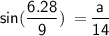
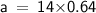
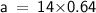
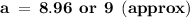
For Side B
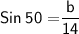
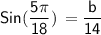
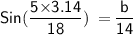
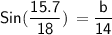
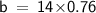
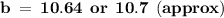
Hence, The value of angle A , side a and b is 40° , 9 and 10.7 .