Question

Does (3,-4) lies on the locus x2+y2=25​

Answer 1

yes! that is correct

Answer 2

Yes

Explanation:

Both arguments are squared so the equation are in the form of a circle.

A lotus is a point that is equidistant from some fixed point of a conic section. This is a circle so the fixed point is called a center of the circle.

The center of the circle is equidistant from any point on the circumference of the circle. In order for a point to be on the circle, it must satisfy the circle equation.

`{x}^(2) + {y}^(2) = {r}^(2)`

Let plug in what we know

`3 {}^(2) + ( - 4) {}^(2) = {5}^(2)`

`9 + 16 = {5}^(2)`

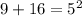
So 3,-4 is on the locus of the circle.